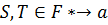USB Oscilloscope

VD Demo

Demonstration of the power of the Voodoo language within the Voodude editor. Voodoo uses large scale functions which translate very little Voodoo code into much larger chunks of C and Java. If there is a function not included within Voodoo you can build it natively just as you would any other C or Java based function.

Project keyStone

Modifying the Heat Equation for Multi Component and Layered Printed Circuit Boards

Introduction

PCB's are excellent for creating multi component electrical systems, especially when they involve IC's or larger components. In this post I will demonstrate a modification of the differential heat equation to allow for accurate modeling of these types of electrical systems, when they are supplied with power or when they are not.

Notation Overview

\ is a special form of and, it is not the same as the Boolean and or , rather it means that X\Y means that X is performed and Y is performed regardless of their condition

Semicolons denote the change from one statement to the next

$ is the length (Rows) of a given matrix: $X$ returns the length of X

The Equations

Suppose we have a single layer of circuit board with an arbitrary number of components, however it contains a particles. In such a circuit board:

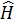 is the Hamiltonian and f represents force based interactions. Supposing that no uniform electricity is flowing in any amount worth mentioning for something the size of a PCB, then a blank pcb is represented by the generic Heat equation:

Note that a is a constant for a single material, such a presumption cannot be allowed to occur in a board with multiple components of multiple materials, note that a fiber glass substrate( the non-electrically conductive piece of the board) will not have the same thermal diffusivity as the copper components. Also, diffusivity can be temperature dependent, just as conductivity is. Therefore:

However before we can operate F* we must design the board in a mathematical context. Supposing that this methodology will be used in a practical application it will be more effective to define components as polygons,lines, and curves rather than defining each element a.

|Copper Line Element|

Creating a copper line element is simple:  ____________ would simply be y=c or x=c or z=c. However suppose we had a connected copper element which behaved as follows (the black line is of interest) which requires a third dimension:

Once cannot simply create a component function which states that the function changes depending upon conditions of x and y. Obviously the loop must be 3 dimensional; therefore we can create a system which auto routes this to the next level.

, in other words for every single value of x and y there cannot be a duplicate of these values on the same plane. Now for the 3-D auto route:

As for a description of P:

 Which is equivalent to:

 |Polygon Element|

|Component|

 Components could range from capacitors and diodes to antennas and heat sinks. Therefore I provide example equations to generate both. Note that the Capacitors and diodes are generally made of multiple materials and are thus shown through the diffusivity of their individual components. 

Heat Sinks

Capacitors and diodes

 The resistance for each region is computed and converted to thermal energy through:

This equation can be made more accurate through measurement of material properties.

The Mathematics of CERN Style Software for a Cloud Chamber

INTRODUCTION

A cloud chamber is an interesting device that allows a user to see charged particles. it consists of supersaturated alcohol and water vapor which is ionized by the charged particle and begins to precipitate. Alcohol is used because its low freezing point allows for us to quickly reach the critical temperature at which ionization will cause precipitation. In this blogpost I will outline the mathematics required for the system, the mathematics for a program to automate detection, and the mathematics of the particles themselves. In an upcoming blogpost I will demonstrate an implementation of the Cloud Chamber and the software.

OVERVIEW

We begin with a brief overview of the particles themselves, as computations from this section will allow for proper design of the chamber, as well as proper mathematics and design of the subsequent program.

    Suppose a particle P was launched at a velocity V towards Earth. It will be attracted to two plates mounted to the outside of the box following the coulomb equation. Also the degree of ionization is a function of the energy and ionization ability of the particle which adjusts the width of the ionized trail, therefore an algorithm can determine a particle type simply by analyzing trail width.

Program NOTATION

Custom Operator: $x$ returns the length of x

Turing Machine: <Machine|Function*|Tape>

Boolean Algebraic Program

The A* function applies the Y filter transform onto c